nNEZOU's Blog

先週の写真教室で、フォーカスのところでコサイン誤差のお話があった。これまで雑誌などでコサイン誤差という言葉が出てきて、何となくこういうことかな、という感覚でいたのだが、この機会に、何故三角関数の「コサイン」が出て来るのか、何故サインでもタンジェントでもなくコサインなのか、検証して見た。

以下はその結果。知っている人は見る必要はありません。あちこち脱線するかも知れないし

まず、コサイン誤差の発生する状況の設定

同じ焦点面(焦平面ともいうらしい)に真珠と豚を配置する。真ん中に豚、右寄りに真珠を配置する構図とし、焦点は真珠に合わせたい

撮影の手順として、カメラを構えたらまず右の真珠に向けて焦点を合わせてロックする。この時の焦点距離をf1とする(上から見た図)

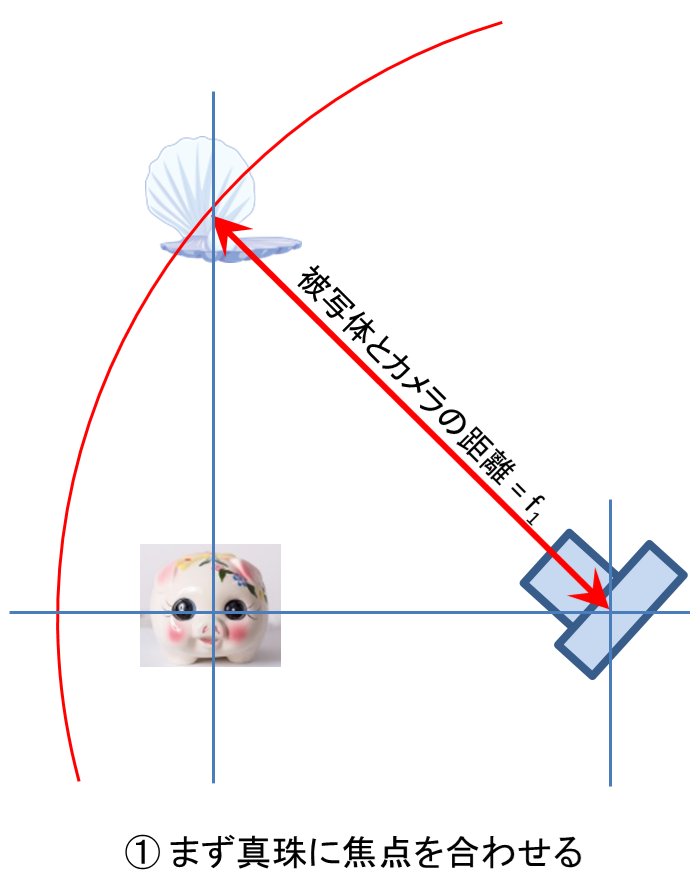
次に、カメラを豚の方に向ける。この時カメラを振った角度をθとする。また、真珠と豚は目的とする構図の同一焦点面にあるので、カメラと豚の距離は、カメラと真珠の距離とは異なって来るはずである。この距離をf2とする

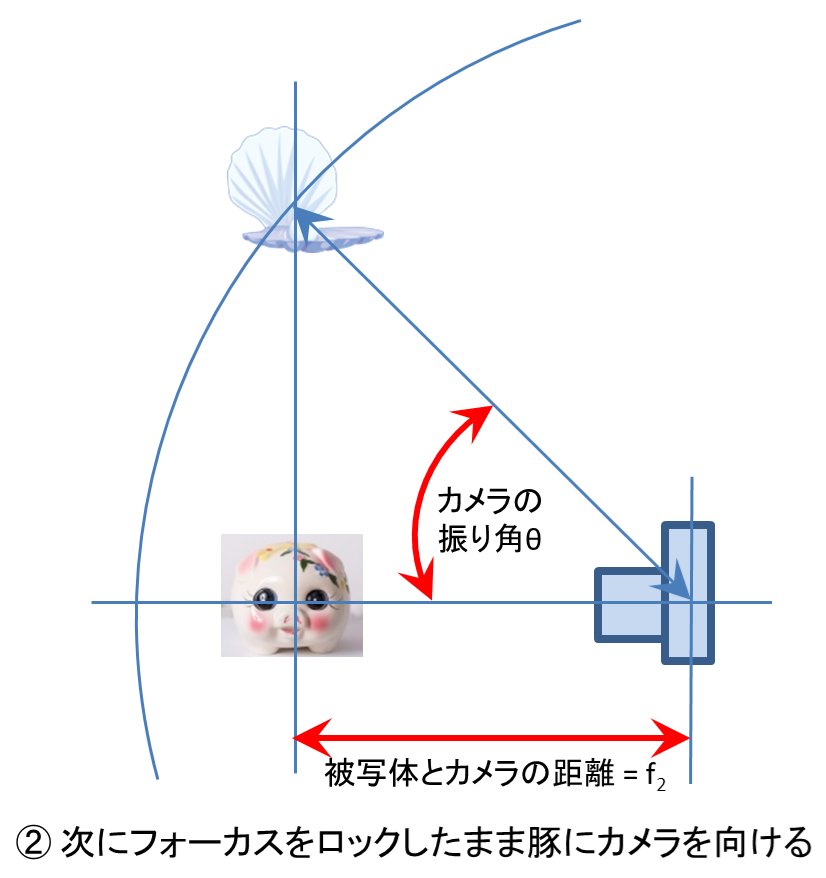
そのままシャッターを切ると、その結果、写真は多分こうなるだろう。豚も真珠もぼける。コサイン誤差が被写界深度を超えた場合は(だよね)

ここまでの理解は、多分正しいのではないか。間違っていたら、これから先の議論が台無しになるので、その場合はそっと教えてほしい。そしたらこの記事もそっと消すから

いよいよこのコサイン誤差の定式化だが、下はこれまでの説明をまとめた図。ここでは、このコサイン誤差は次のように定義する

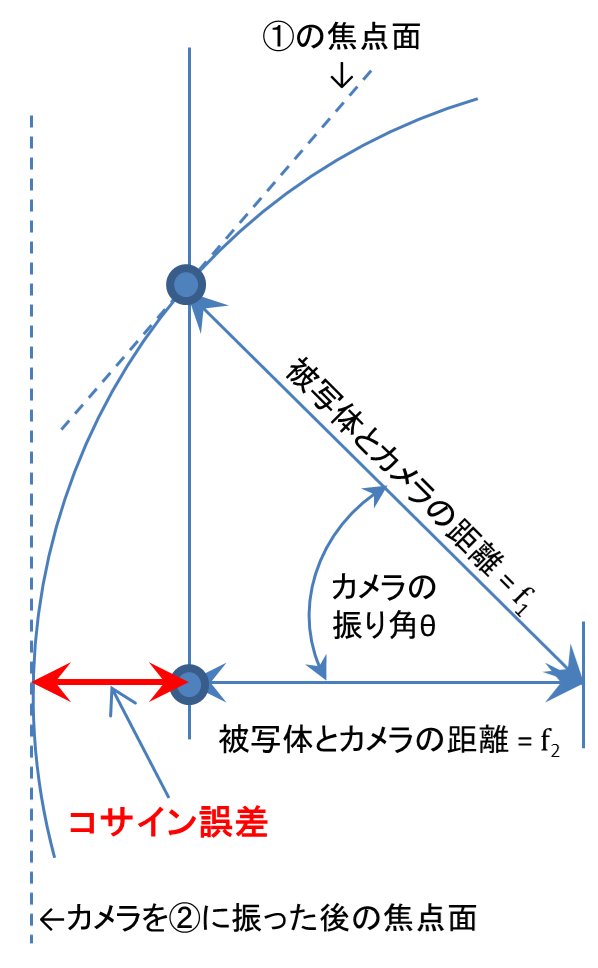
コサイン誤差(仮にεとする) は、 真珠に合わせた焦点距離 (f1) と、正面の豚とカメラの距離 (f2) の差

ε = f1 – f2

となる。ここで

f2 = f1 cos (θ)と表現できるから、

ε = f1 (1-cos(θ))

と表現できる。なるほど。このように三角関数のcosineを使って表現できるからコサイン誤差というのだ

試しに、f1=1000mm、θ=30° としたらコサイン誤差はどれくらいになるか計算したら、約134mmとなった。これと実際の被写界深度を比較して見る。例えば、50mmの標準レンズをF8に絞った場合

前方被写界深度 87.59 mm
後方被写界深度 106.19 mm
被写界深度 193.78 mm

となり、豚も真珠も焦点面より前にあるので、多分前方被写界深度が適用されるだろうから、87.59mmに対してコサイン誤差134mm、全然ダメということがわかる

ひとつすっきりした

と同時に、被写界深度は前方と後方が異なるということがわかってしまった。この物理的直観がつかめないという課題が…

※ 被写界深度の計算には 「keisanサービス」https://keisan.casio.jp/exec/system/1378344145 のお世話になりました

2020/08/09
んねぞう