nNEZOU's Blog

フィボナッチ数列の隣り合った数の比が、黄金比に漸近するという話をYouTubeで言っていた。何のことかと言うと…

■ フィボナッチ数列とは

下記の数列を見て欲しい

0, 1, 1, 2, 3, 5, 8, 13, 21…

第一項はゼロ、第二項は1を初期値とする。第三項は、第一項のゼロと第二項の1の和とする。同様に、第4項は第二項の1と第三項の1の和とする。以下同文。このような数列をフィボナッチ数列と言う。一般項(漸化式)は下記のように書けるか

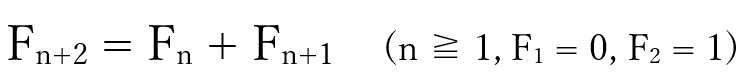
自然の諸現象にもその数列に従っているものが多くみられるという

■ 黄金比とは

私の場合は写真や絵画の構図の話の時によく聞くが、具体的には、1 : 1.6180339887…と言う比の形。右の1.6180339887…は無理数で、黄金数と言うらしい。数字の字面はともかく、この数字に何の意味があるかについては私の知っている範囲でもこんなところに書くスペースもないので、各自検索して欲しい。すごく深い森が待っていると思う

問題は、上のフィボナッチ数列の一つの項が、その前の項の何倍になっているかの比が、この黄金数にだんだん近づいて来る、というもの

実際にフィボナッチ数列と、その各項が一つ前の項の何倍になっているかをPythonで計算させて、Excelでグラフにしてみた

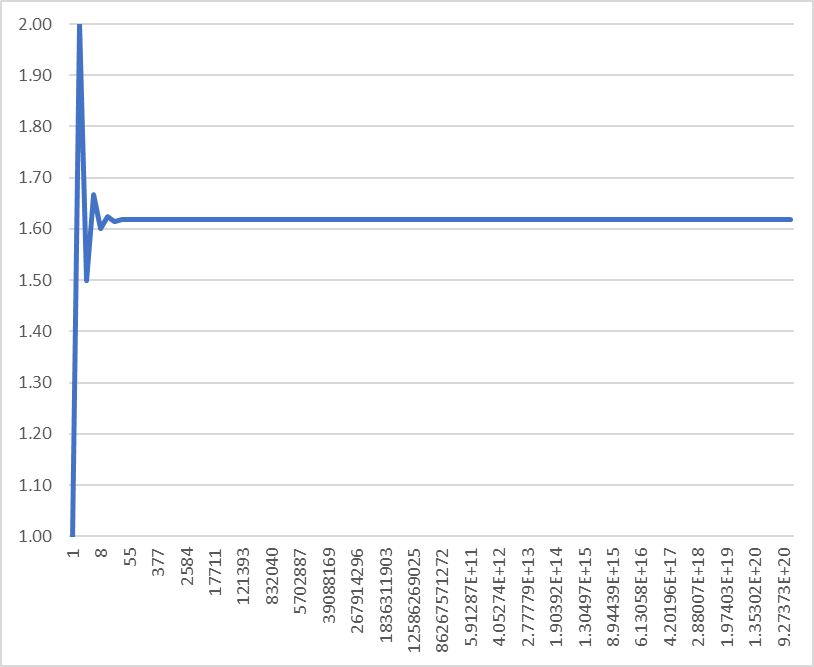
まず一般に使われるであろう1 : 1.618の値に対して、フィボナッチ数列13項めの144で1.61797、14項めの233で1.61805となり、割合早く収束するのだな、と言うことがわかった

この収束の波形を見ていて、ひょっとして音響として再生してみたら、何か深遠な自然の真理を垣間見ることができるかも知れないと思い、最初の部分だけを抜き出して見た(1.6180…を0Vにシフトしてある。また、このままの電圧だとスピーカーが壊れるので、正規化が必要かも知れない)

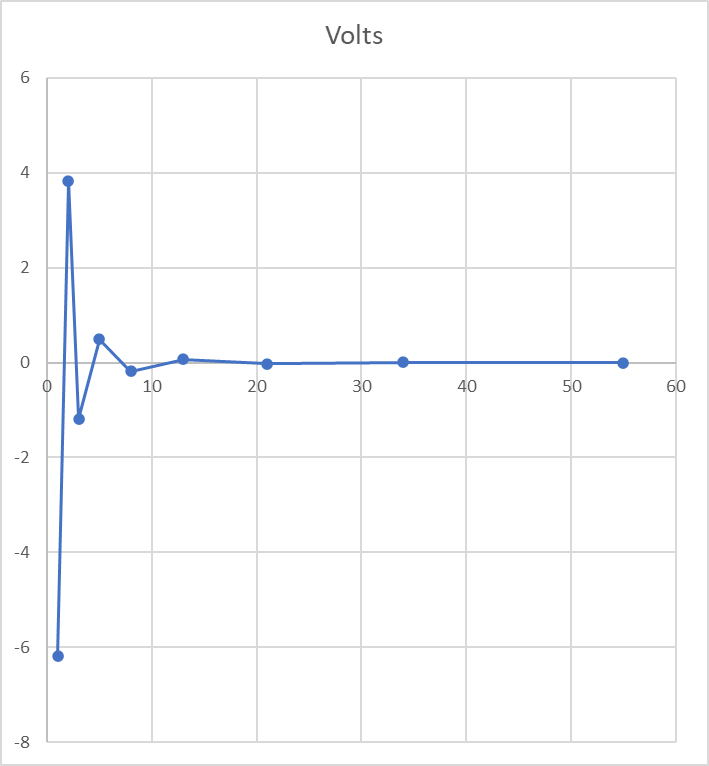
だけど、苦労して再生して見ても、「プッ」とかいうしょぼい音で終わるような気がしたので、やめておく

関係ないが世の中には電圧波形を見ただけでどういう音がするかわかる能力を持った人がいてもおかしくないような気がする。うん、これは1980年、カール・ベームが振ったウィーン・フィルのベートーベンの5番だな、燻銀の響きがするぜよ、とかコメントする…

さらに言うと、このフィボナッチ数列って、Excelで簡単に作れて、比の計算も一気にやれるんじゃね?と言うことに今気が付いた

いやいや、この数列を定式化して、プログラミングすることに意味があるのだ、と言うことでソースコード

a = 0
b = 1
c = a + b

# ファイルを開く（書き込み用）
with open("phi.txt", "w") as file:
    while c < 1000000000000000:
        a = b
        b = c
        c = a + b
        phi = c / b
        # コンソールに出力
        print(c, phi)
        # ファイルに書き込み
        file.write(f"{c}, {phi}\n")

本日の教訓

ここに書いた一連の処理はExcelでOne thoughでできることに後で気が付いたが、アルゴリズムを考えてプログラムすることに意義があるのだという言い訳が見つかって良かった

2025/06/14
んねぞう