nNEZOU's Blog

近くの公園で、写真教室が開催されていることを2年前から知っていた。ずっと迷っていたが、4月に基礎コースの募集があったのを機に申し込んだ。毎月2回の教室で、今日で既に3回目になった。講師はプロのフリーカメラマンで、映画とスチル写真の両方を経験し、さらに映像関連、 映画評論 の著作/翻訳、同人誌の編集長など幅広く活躍されており、私などからは音楽で憧れの東京藝大の講師なども務められている方だ。

受講者の方々も幅広い年齢層からで、楽しくやっていければ良いと思う。

最初に、高い機材があれば良い写真が撮れる、また写歴が長ければ長い程良い写真が撮れると言う考えは大間違いだというお話。 カメラの持ち方、構え方、そしてレンズの焦点距離と画角の関係。7月には作品の展示会があるそうだ。基礎からしっかり学んで、構図、階調等についての考え方、見方を身に付けて実践に適用できるようになりたい。

焦点距離と画角の関係について。焦点距離と画角は反比例するということを学んだ。これに対して、私は、後で考えて大汗もののアホ発言をしてしまった。これを知りたい方は次の「Read the rest of this entry」をクリックしてください

私の問題発言
「先生、画角と焦点距離は反比例することは理解しました。それでは、焦点距離が半分、即ち画角が倍になると、写る範囲は縦2倍、横2倍で4倍になるわけデスネ」

この発言の何が問題か
画角が倍になると、写る範囲が4倍になるという二乗則は成り立たない
以下、その証明

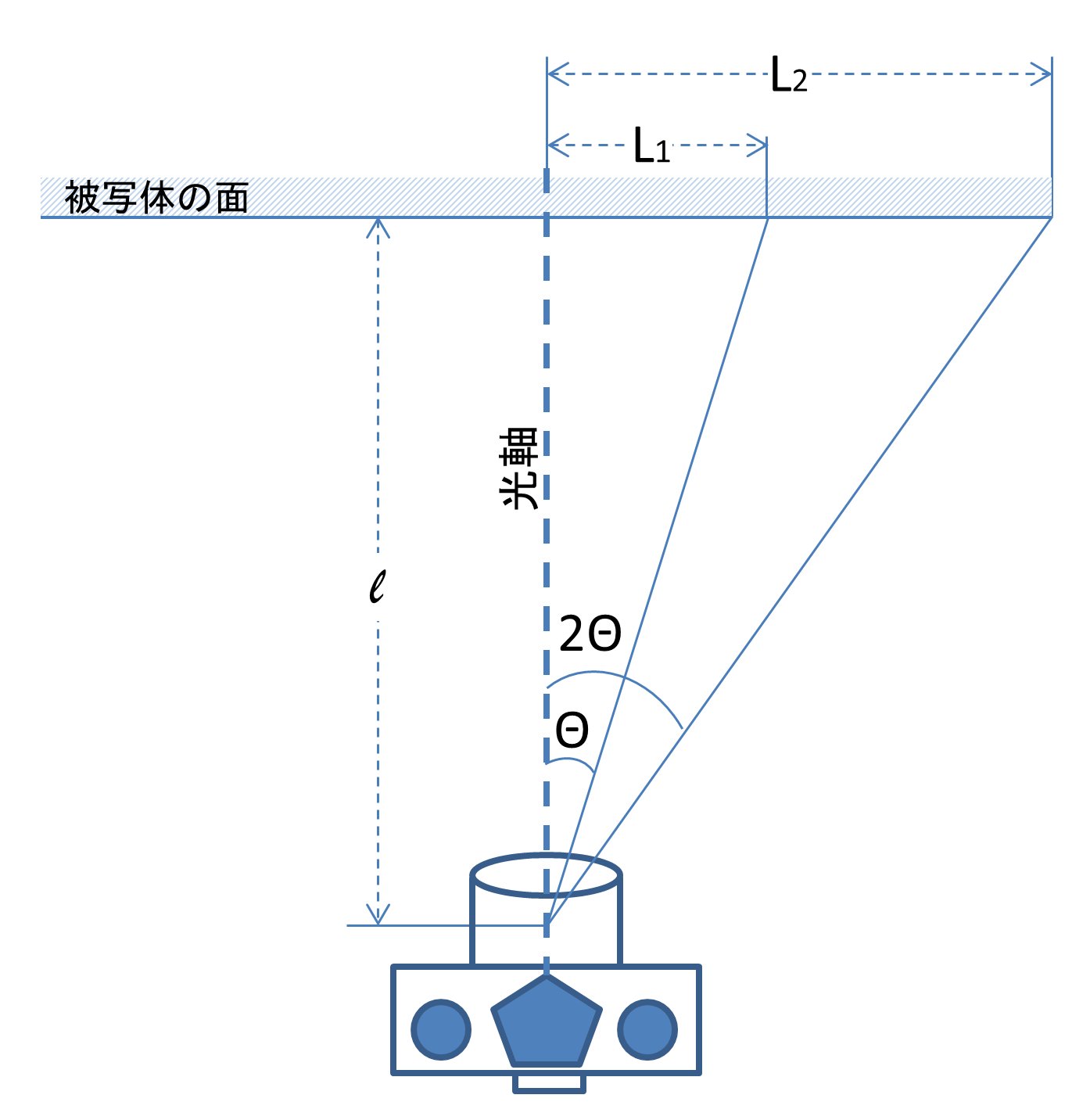
簡単のために、上から見た図で説明する。また、対称のために光軸の右半分について論ずる。下図のように、レンズと被写体の距離をl、画角をΘとする。この時、レンズで写せる範囲をL1とする。

L1は下記の式(1)で表される。

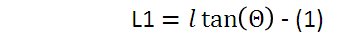
もし、私の説が正しければ、画角が倍になった時のレンズで映せる範囲L2は、下記の式(2)で表されるはずである。

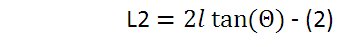
一方、L2はtangentの定義により、式(3)によっても表現される。
ここでは、自分の説が正しいことを証明するためには式(2)と(3)が等価であること、即ち式(4)が成り立つことをを示せば良い。

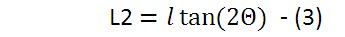
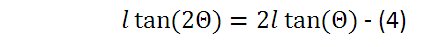
一方、良く知られている2倍角の公式(5)を見ると式の形が異なっており、一目見ても式(4)は正しくない。

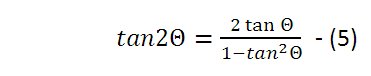
これにより、私の主張した式(4)は正しくないことが証明された。考えて見れば自明の話。因みに、近似的に適用できる範囲はどうかを探るため、表計算ソフトで計算して見た。

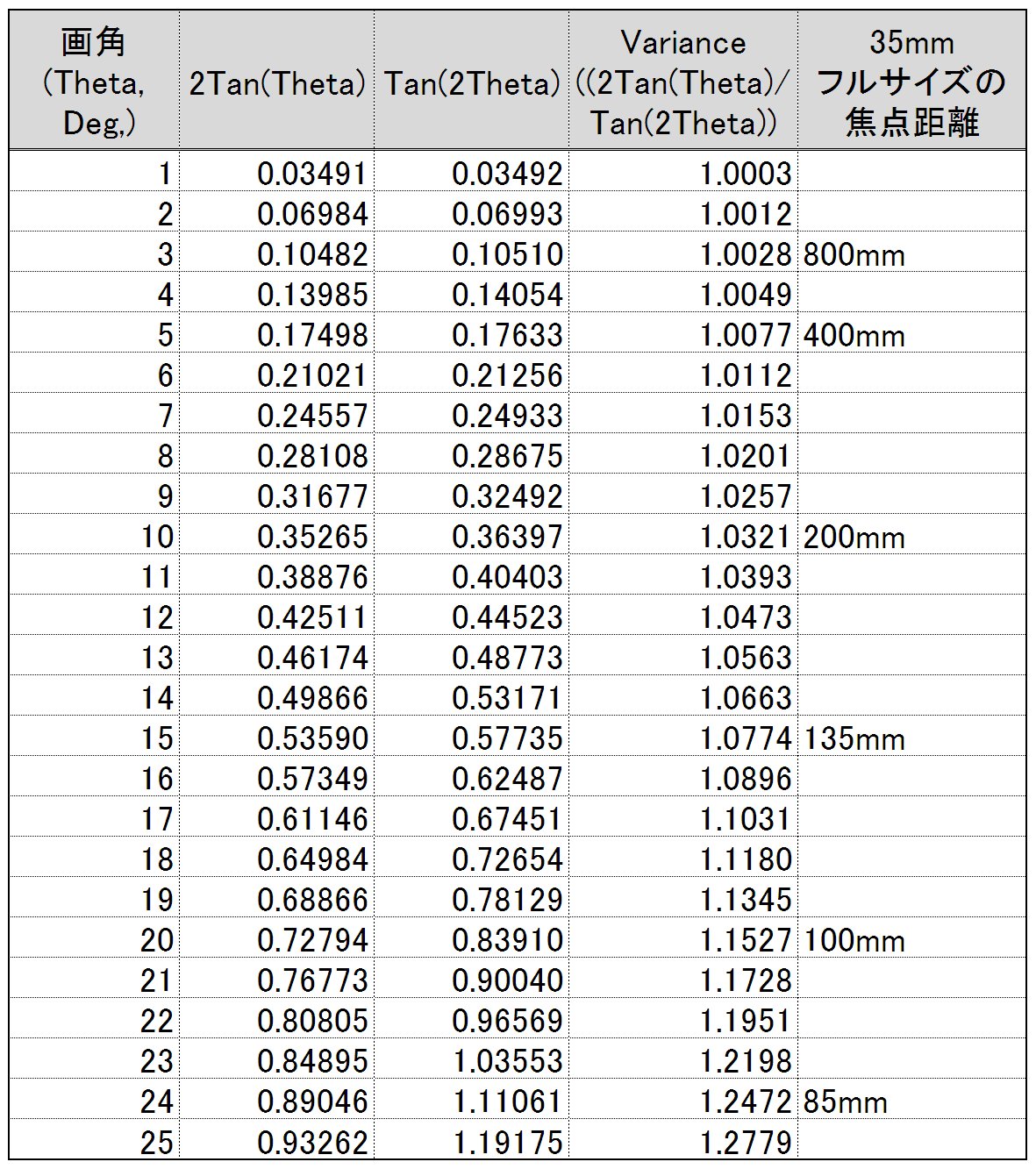
表の読み方
Tan(2Theta)の列は、仮に現在のレンズの画角が2倍に変化した場合のTangentの値である。2Tan(Theta)は現在の画角に対応するTangentの値を単純に2倍した値である(要するに私の似非理論)。
Varianceの列は、私の説であった水平角と撮影面が比例するとした場合と、実際の撮影面の比率を計算したもの。例えば焦点距離800mmのレンズの画角が倍になった場合、正しい計算式と似非理論では水平方向で0.28%の差が生ずることを表している。85mmのレンズでは水平方向で既に25%の差が出ていることがわかる。

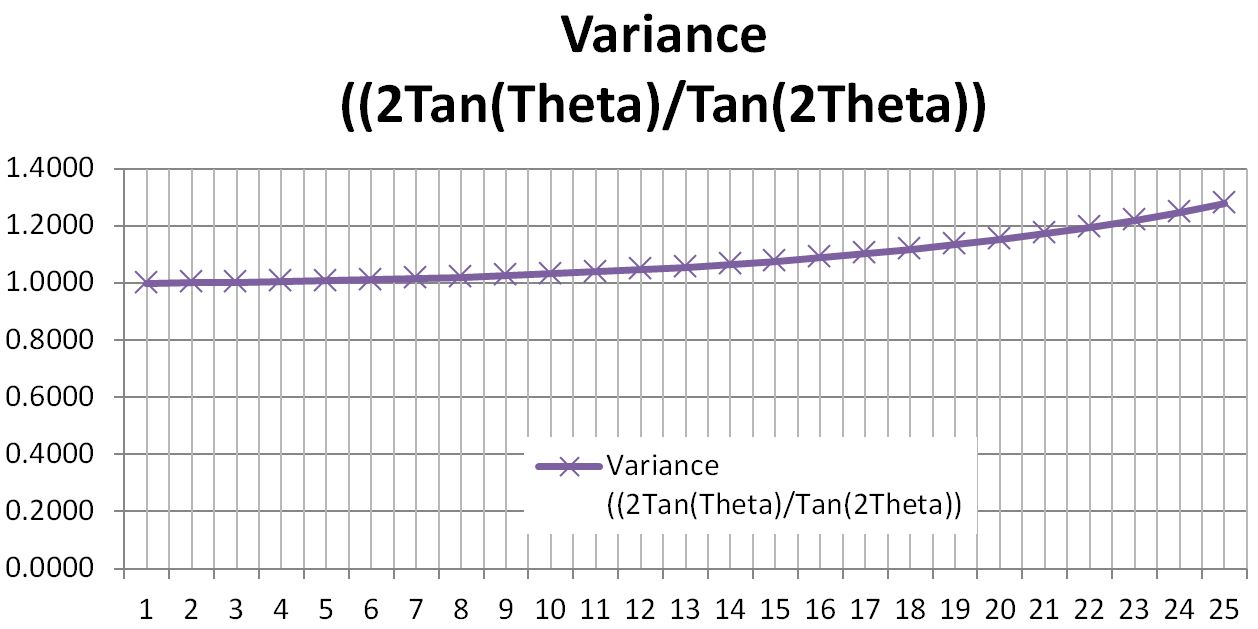
私の似非理論が通用するのは、撮影面がカメラを中心とした円筒形である時位のものだ。しかし、これが垂直方向も考慮にいれた場合、球面を扱う必要が出て来て、その場合の面積の計算はどうなるの?、平面への投影方法は?とか泥沼にはまるのでこのあたりで退散する。

こんな的外れの発言をする受講生ですが、先生、よろしくお願い致します

m(_ _)m

2019/05/06
んねぞう