nNEZOU's Blog

Sod’s LawのRisk Factorの計算式で、それぞれのパラメータ(U:Urgency ,C:Complexity,I:Importance, S:Skill, F:Frequency)がどのように寄与するのかざっと確かめて見た。以下はそのレポート。Sod’s LawおよびRisk Factorの計算式等については以前のエントリーのSod’s Law のRisk Factor 計算式とSod’s Law の Risk Factor計算を参照されたい。

1. 手法

各パラメータのすべての組み合わせで計算させるためにBasicで簡単なプログラムを組んで値をcsvで吐き出させ、これをExcelに読み込んで散布図などを描かせてみて考察する

2. Fact

恥ずかしながらソースコード。

10 PRINT ” u c i s f r1 r2 r3 r4 r”
20 FOR u= 1 TO 9 STEP 1
30 FOR c= 2 TO 8 STEP 1
40 FOR i= 1 TO 9 STEP 1
50 FOR s= 1 TO 9 STEP 1
60 FOR f= 1 TO 9 STEP 1
62 r1=u+c+i
64 r2=10-s
66 r3=sin(f/10)
68 r4=20*(1-r3)
70 r=0.7*(u+c+i)*(10-s)/(20*(1-sin(f/10)))

80 PRINT u,”,”,c,”,”,i,”,”,s,”,”,f,”,”,r1,”,”,r2,”,”,r3,”,”,r4,”,”,r
90 NEXT f
100 NEXT s
110 NEXT i
120 NEXT c
130 NEXT u

(r1~r4は途中検算のための値なので、下記に掲げる結果には入れていない)

この結果の生データはここ(csv)Sods Risk factor 。

全部で45,927通りの計算となった。

U:Urgency 1~9

C:Complexity 2~8

I:Importance 1~9

 S:Skill 1~9

F:Frequency 1~9

の範囲で都合9×8×9×9×9=45,927。

上記のすべてのパラメータについて、Excelでも同様にRisk factorの計算式を組み込んで比較したが、整数はすべて一致、実数は差が10^^-10(10のマイナス10乗)以下であることを確認している。

3.考察

3.1 結果の分析

Risk factor(以降RF)の最小値は0.155267(1, 2, 1, 9, 1) (括弧内は(U, C, I, S, F)の組み合わせ)

緊急度最低、最も単純で、重要でなく、スキルもいらず、めったにない仕事がリスクが低い

最大値は37.79888(9, 8, 9, 1, 9)

逆に緊急度が高く、複雑で、重要で、スキルが必要で、頻繁に行われる仕事はリスクが高い

下の図はRFのヒストグラム。最頻出の値はRF2ポイント台で、RF2.06までの値は全体の20%。RF4.67までで全体の50%、RF12.63までで全体の90%を占める。

全体の99%を占めるのはRF23.26までの範囲である。

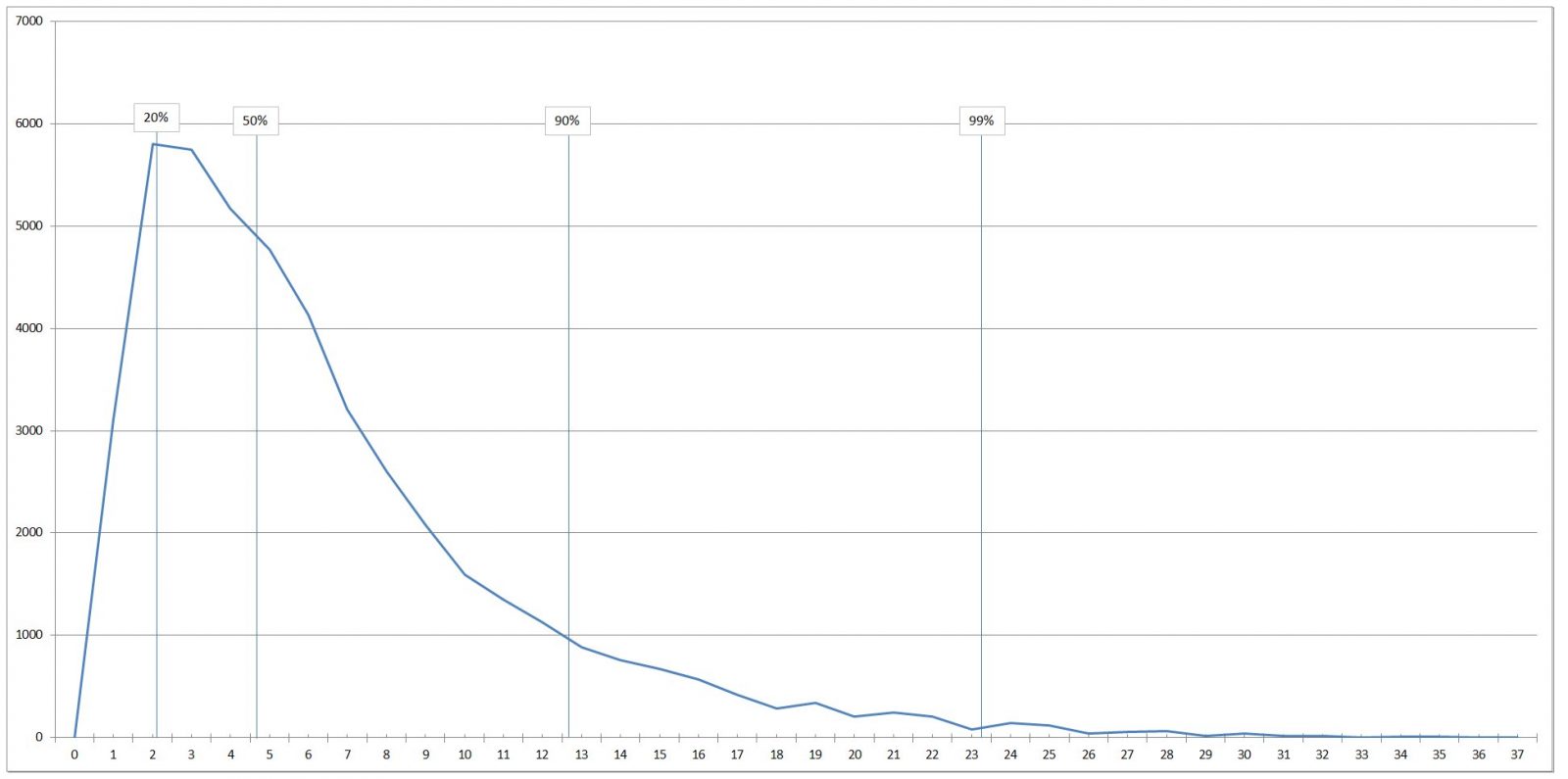
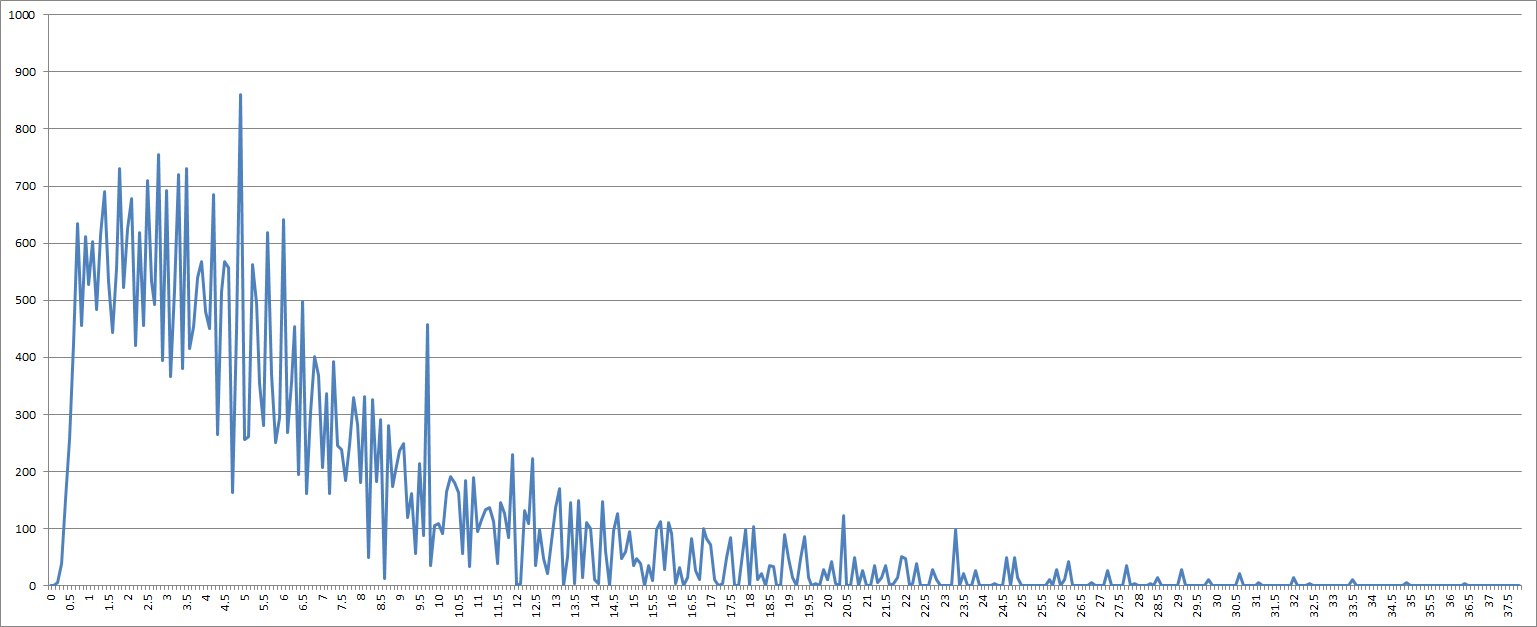
RF2までのグラフのカーブの立ち上がりが急なので、横軸の単位を0.1刻みにしてみたものが下の図。

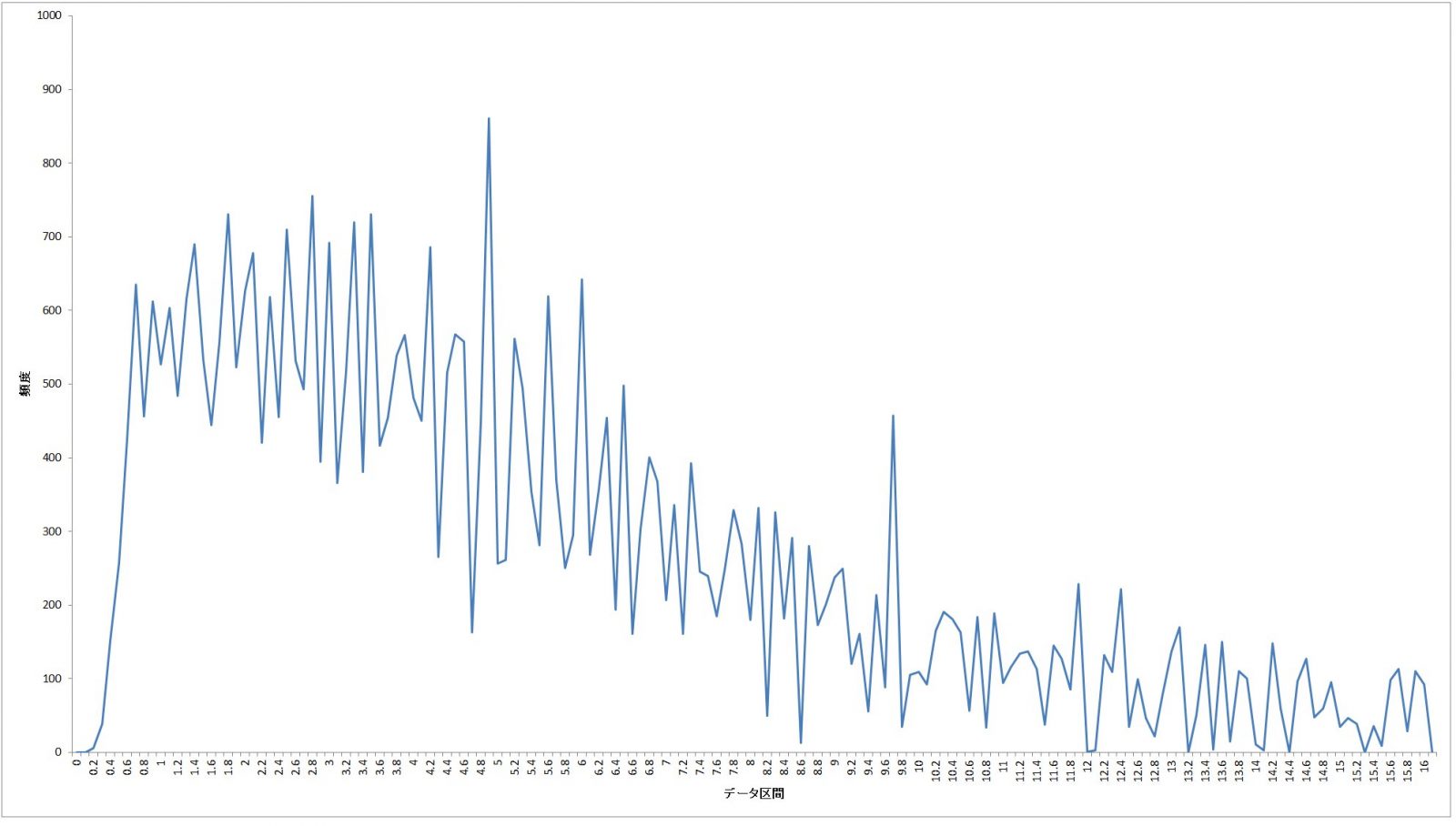
さらに0~16の区間の拡大

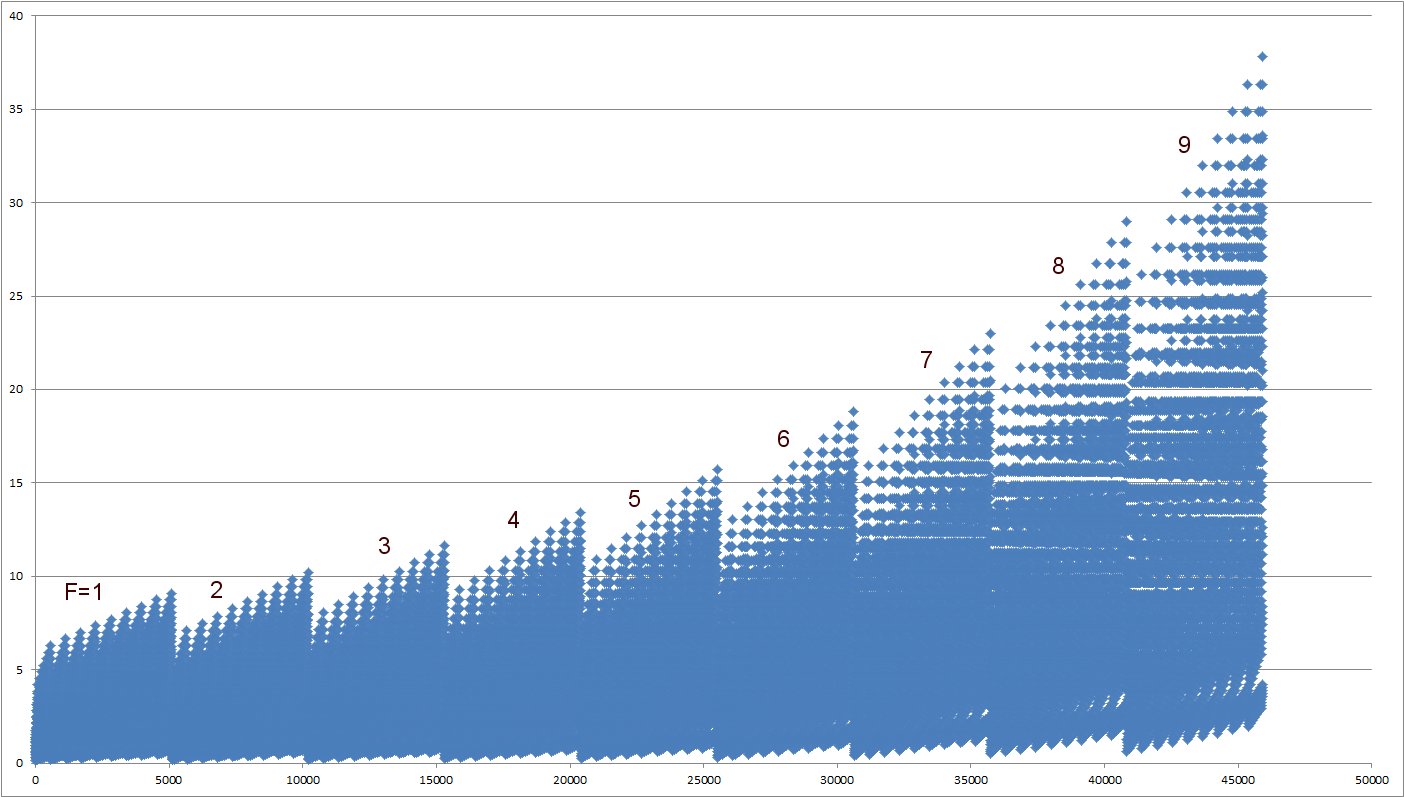
Fによる寄与を見るために、Excelで散布図を作って見た。データをFの昇順にソートして、縦軸にRFを取った。鋸の歯状の形で左からF=1,2,3…となる。Fの値が大きくなるにつれて、即ち頻度が増すごとに、Risk Factorの上限が加速度的に上昇してくることがわかる。

各パラメータの寄与については、U,C,I,S,Fは数式上リニアに効くことがわかるので、特に散布図は不要と思う。

3.2 日常への適用

これらをもとに、実生活での応用において、どのような適応ができるかいくつかの例を用いて考察する。まずRFの最低値は、上述したように

0.155267(1, 2, 1, 9, 1) (括弧内は(U, C, I, S, F)の組み合わせ)

である。

ケース①

それでは、逆に極限状況として、下記のような状況を想定して見る。

自分が大型旅客機に乗っていて、着陸の直前に機長、副操縦士が二人とも病気になって操縦できなくなり、自分がとにかく何とか着陸させなければどうしようもないという、まるで映画みたいな絶体絶命の場面だったとする。この場合、各パラメータは下記のようになるだろう。

緊急度    Urgency=9 最高の緊急度
複雑さ    Complexity=8 最高の複雑さ
重要性    Importance=9 最高の重要度
スキル    Skill=1 最低のスキルレベル
頻度        Frequency=1 滅多にない

このRF値は7.372となる。

仮に、ここでF(頻度)を9(毎日)とすると、RF値は37.799に跳ね上がる。

F:の定義は、Frequency: how often do you have to do this ?ということであるから、自分的にはこんなことは一生に一度あるかないかの事象なので、F=1と置きたい。常識的に考えて、このような事態で生きて帰って来れるとは到底思えないので、F=1で十分だ。

ということで、一応このRF7.372以上は成功は絶望的な領域に入るとする。(Boeing 737と結びつけると覚えやすい? 覚える必要もないが。)

ケース②

次に、日常生活の上で、奥さんを買い物のため大都市郊外の自宅から最寄の私鉄の駅まで車で送る場合について計算する。

緊急度    Urgency=3 本人にとっての緊急度はわからない。自分的には普通
複雑さ    Complexity=2 道は単純、道幅はそれほど太くはなく片側1車線、交通量もそれほど多くない
重要性    Importance=3 普通
スキル    Skill=6 車の運転については問題なし、かといってプロ並みの安全運転スキルがあるかと言えば否
頻度        Frequency=6週に2,3回

このRF値は2.573となる。この値を日常生活のひとまず基準値としておこう。

ケース③

日常生活の、少し大変な局面についてはどうか。

雨の日の夜、急用で、大都市郊外の自宅から大都市中心部まで車で行かなければならない。途中高速道路もある、と言う状況。

緊急度    Urgency=7 急用だから。
複雑さ    Complexity=5  道順は複雑、初めて走る経路が含まれている。高速道路のジャンクションで合流、分岐があり、迷いやすい
重要性    Importance=7 急用だから
スキル    Skill=4 車の運転については問題ないが高速道路には慣れていない
頻度        Frequency=1 滅多にない

このRF値は4.433となる。

ケース④

最後に、自分が小規模なバロックアンサンブルのコンサート(聴衆が100人未満)でバッハの2つのヴァイオリンのための協奏曲第一楽章の第一ヴァイオリンのソロを(音楽的中身は別として)何とか無事に弾き終えるというタスクについて評価して見る。

緊急度    Urgency=7 もうステージに立っているのでやっぱり止~めた、とは言えないし
複雑さ    Complexity=7 自分的に難易度高、しかしタルティーニみたいに絶望的でもなし
重要性    Importance=7 これで失敗したらビールが飲めない(飲むけど)、夜寝られない
スキル    Skill=7 一応何度も練習を重ねている。自分としても、まあ大丈夫だべ、という気でいる
頻度        Frequency=2 年に一度あるかないか

このRF値は2.752となる。

3.3 考察のまとめ

以上を表の形にまとめて見ると、次のようになる。

ごく日常レベル	2.573
日常の緊張を要するレベル	4.433
非日常で頑張らなければならないレベル	2.752
絶望レベル	7.372

これを見て意外に思われたのは、「非日常で頑張らなければならないレベル」が、「日常の緊張を要するレベル」よりかなり下であること、そして「ごく日常レベル」に毛の生えた程度であること。非日常だから、思いっきりRFが高いかと思っていたのだが、考えて見たら、事前にそれなりの準備を重ねていれば、リスクはそれほど高くないのだ、ということだ。

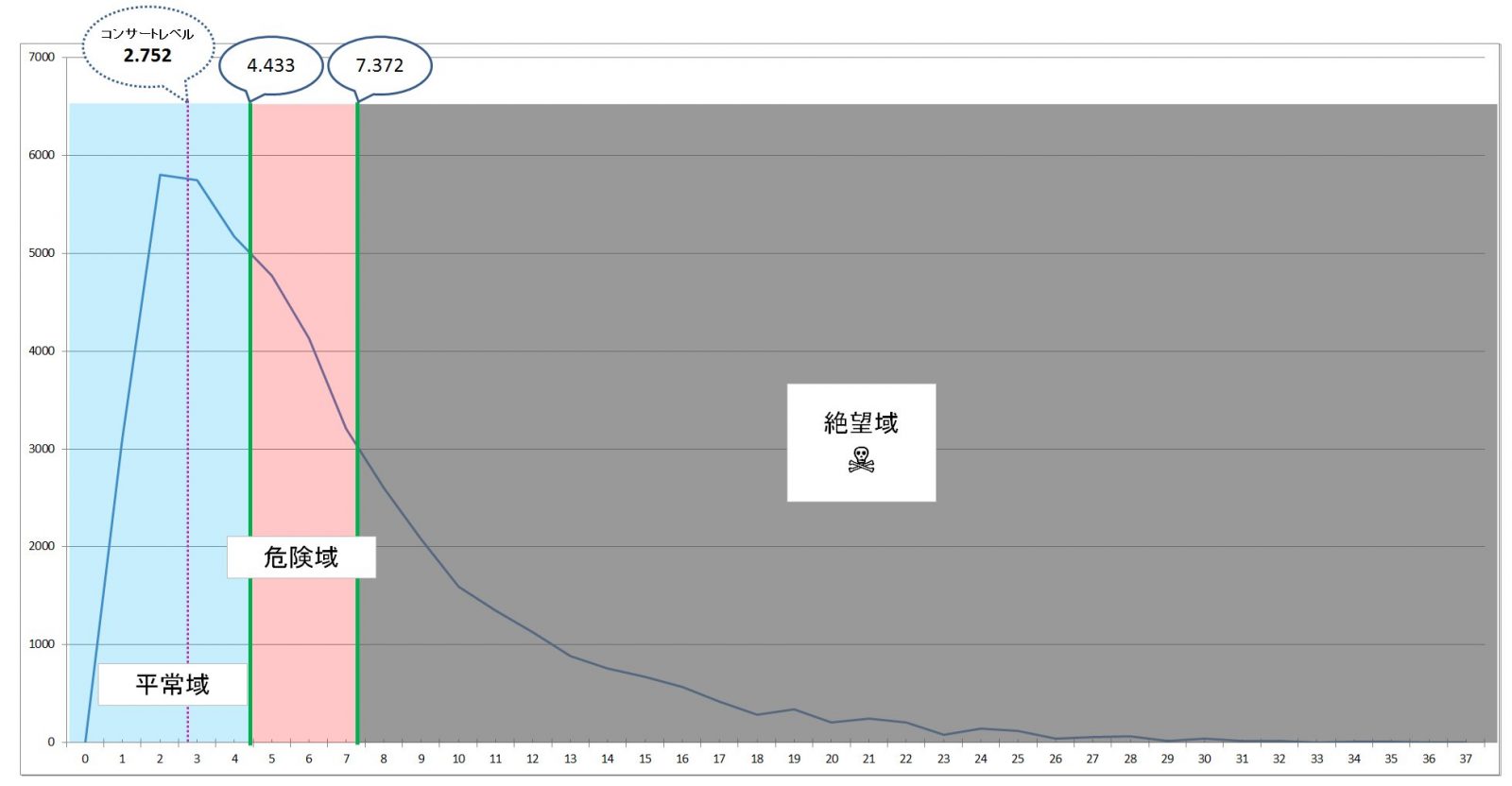
この知見をもとに、上に掲げたヒストグラムのゾーン分けをして見た。

参考までに、RF4.433以下の事象は全体の47.76%が含まれる。コンサートレベルのRF2.752以下の事象は全体の28.85%が含まれる。

以上により、ここでは日常生活に対する適応として、下記のようにまとめることができる。

ごく日常レベル	~2.573
非日常で頑張らなければならないレベル(コンサートレベル*)	2.752
日常の緊張を要するレベル	~4.433
危険レベル	~7.372
絶望レベル	7.372~

*ここでは「日常の緊張を要するレベル」の例としてコンサートを挙げたので、特にこのレベルを「コンサートレベル」と呼ぶことを提唱したい。

4. 結論

1. 各パラメータのうち、Fの値の増加がRF値の上昇に加速度的に効く。また頻度が多ければ多い程リスクが増す方向に作用する。その他のパラメータは数式の形からリニアに作用する。
2. 日常生活への適用において、RF7.372以上のケースは、成功は絶望的と考えるべきである(Boeing 737…まだ言ってる)。また、そうでなくてもRF4.433以上となるようなタスクは極力避けるべきである。
3. 日常の短距離の人の送り迎えを基準とすると、準備をそれなりにしていれば、非日常的コンサートも、奥さんの送り迎えプラスアルファ的なレベルと言うことになることが分かった。このレベルをコンサートレベルと呼ぶことを提唱する。

5. あとがき

準備をそれなりにしていれば、非日常的コンサートも、奥さんの送り迎えプラスアルファ的なレベルと言うことになる。非日常的なことだから人間、緊張はする、しかしこういう風に客観的に評価して、知っておくと良い結果が得られることに繋がるのではないだろうか。

計算を実行させるために、最初はiPadで動くBasicインタープリタを使ってやってみたが、計算のループが4層以上になると途中で落ちるため、Windows上で適当なものを探し、MicrosoftのVisual Studioが良いということでイントールしようとしたらインストールに致命的なエラーが発生して使えなかったりして、結局JavaScriptを使ったWeb上のインタープリタサービスを使わせてもらった。昔学生時代にNECのPC98シリーズでBasicを使っていたことがあったので、この記憶を辿りながらぽつぽつと入力したが、元来が緩い頭なので、厳格に文法を守らないと受け付けてくれない機械相手に、しばらく楽しませてもらった。

やっと計算ができてデータをExcelで分析する段になって、散布図については、素のExcelに元からあったメニューにあったので、何とか作成できたが、ヒストグラムについては「分析ツール」と言うアドインが必要なことがわかった。また、ヒストグラムの作成方法もわかった。これは今後何か役に立つかも知れない。

2017/06/22

んねぞう